Book Tour
This page provides a brief overview of the overall flow of the book. Elsewhere on the site, you may find a detailed table of contents, examples of specific chapters, and examples of specific programming exercises. The figures on this page are taken from the 150+ figures in the book, with each figure number indicating the corresponding figure in the book.
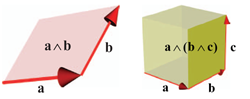
Part I introduces the basics of geometric algebra. It provides the algebraic structure, with products inspired by the desire to represent linear subspaces and geometric operations on them. Throughout, the concepts are illustrated and developed through drills, structural exercises, and programming exercises.
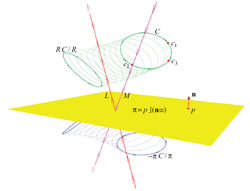
We use the blades of a geometric algebra to algebraically represent all geometrical primitives. The scalars in a vector space are represented as 0-blades, the vectors by 1-blades, and the oriented area elements are 2-blades. In Part II, we will give enriched interpretations to these blades. For example, in the homogeneous model 2-blades are used to represent lines and 3-blades represent planes; in the conformal model 3-blades represent circles, and so on.
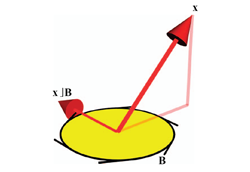
In this chapter, we also introduce dualization. Any element in geometric algebra has a dual representation, through its inner product relative to the total volume element of the space. Those 'geometrical complements' are often very convenient in computational expressions.
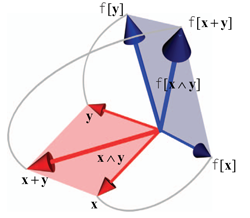
These linear transformations preserve the properties of the outer product, and are hence called outermorphisms. This chapter is a bit algebraic, but it is important to know how the subspace products transform under linear transformations.
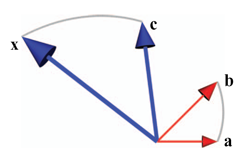
The geometric product is invertible, and this immediately simplifies the algebraic specification of a specific geometrical situation. You can divide by vectors, and in the planar example of Figure 6.2, you can use this capability to solve the equation x/c = b/a immediately as x = (b/a)c. Therefore the vector ratio (b/a) defines an operator that rotates and scales.
Chapter 7: Orthogonal Transformations as Versors describes how the most important
generic use of the geometric product is by 'sandwiching' an object X
to be transformed between a versor V and its inverse:
X -> V X /V.
This is a universal, structure-preserving representation of the action of an operator onto any element:
The transform of a geometric combination of elements equals the combination
of the transforms of the elements. Any framework for geometry should
obey this; what is nice about geometric algebra (used properly) is that it
has this structure preservation inherently built in: its operators have this property,
so no computational effort is required to make it true.
(Actually, only orthogonal transformations have this desirable property; but in Part II we show techniques
to ensure that important geometrical transformations become orthogonal in their representing algebra.)
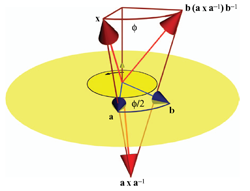
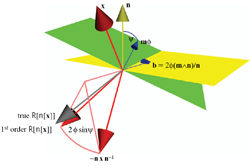
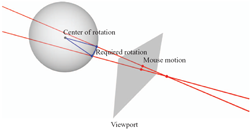
The most basic versor is a vector v, and the associated transformation a reflection in
the plane perpendicular to v. Multiple applications of such versors then generates rotation
versors, a.k.a. rotors, see Figure 7.2. These have all the properties of complex numbers and quaternions,
but now in n-D and universally applicable in a real vector space context.
When formulated with geometric algebra, it becomes possible to differentiate not only with respect to a scalar (as in real calculus) or a vector (as in vector calculus), but also with respect to general multivectors and k-blades. The differentiation operators follow the rules of geometric algebra: they are themselves elements to differentiate dependencies, but must use the non-commutative geometric product in their multiplication when applied to other elements. As you might expect, this has precisely the right geometric consequences for the differentiation process to give geometrically significant results.
In this book, we only give the basic principles, to allow you to interface with other texts that contain a more complete differential geometry in the GA formulation.
Chapter 9: Modeling Geometries introduces the procedure of Part II: we will use the structure of geometric algebra introduced in Part I to model different aspects of geometry. As we do so, we are able to apply it to specific situations, permitting increasingly useful programming exercises.
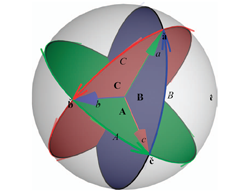
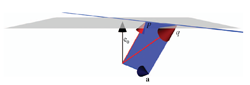
The outer product between two 1-blades representing geometric points is the 2-blade that represents the geometric line between those points (see Figure 11.2b). Naturally equivalent representations of the same geometry (such as by a point and a direction vector) become algebraically identical elements.
The homogeneous model connects well to existing software for computer graphics and computer vision, and we demonstrate that by the programming examples of this chapter.
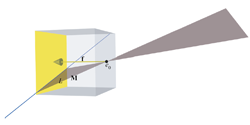
Classically, the former is treated by Plücker coordinates, which then seem like a separate and non-intuitive trick; we show what they actually are, and how the algebra of the homogeneous model empowers the user to span and intersect flats generically.
Imaging by (multiple) cameras in its usual treatment gets obscured by the need to represent the relevant operations in coordinate form; here, too, the homogeneous model provides algebraic insight into the straightforward essence of the geometry-based techniques.
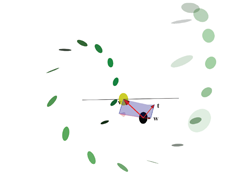
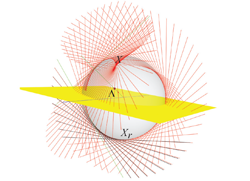
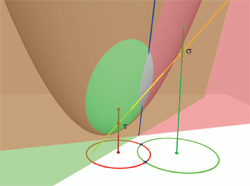
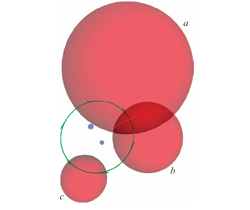
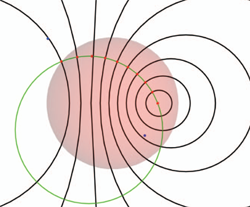
We also give the geometry behind the algebra of the conformal model, and show in detail how the universal meet of flat subspaces can perform the intersection of circles and spheres.
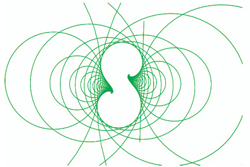
We show how all the various concepts of a 'vector' in classical geometry now have found their specific expression in the conformal model. Normal vector, position vector, free vector, line vector and tangent vector now all automatically move in the correct way under the same Euclidean versors. This demonstrates clearly that the conformal model performs both the geometrical computations and the 'data type management' required in Euclidean geometry.
Chapter 17: Operational Models for Geometries sums up the principles that guided the design of structure preserving models in Part II, and makes an inventory of geometries for which we know such operational models. More will presumably be found, all obeying the same design principles - the conformal model is merely the first.
To use geometric algebra as an actual specification of efficient code in geometric applications, you need to think carefully about its implementation. The conformal model of a 3D Euclidean space uses a 32-dimensional geometric algebra, and a naive implementation would be prohibitively slow. In this Part III, we show that you can use the structure and sparseness of geometric algebra to compete in efficiency with the usual, coordinate-based, hand-coded minimal solutions for applications such as ray-tracing. The coordinate-free specifications in the geometric algebra code then truly acts like a high-level programming language for geometry.
We make an inventory of the issues in Chapter 18: Implementation Issues, focusing on the various levels of the algebraic structure in a typical application. Each of those levels is subsequently treated in a separate chapter. (We also briefly mention alternatives to our preferred approach, and why they are in general inferior.)
In Chapter 19: Basis Blades and Operations we encode the elements of the additive basis for blades efficiently in a bitmap and give algorithms for the basis products of such basis elements.
Chapter 20: The Linear Products and Operations then gives two methods to compose the linear products (outer product, contractions and geometric product) from the results on basis blades. The mathematically pure use of the linear algebra structure of geometric algebra (as a Clifford algebra) in a matrix implementation is just not good enough; processing a 'list of basis blades' is more efficient.
In Chapter 21: Fundamental Algorithms for Nonlinear Products, we process the more awkward operations of geometric algebra, such as inverses and the meet and join products. This involves giving algorithms for factorization (both in terms of outer product and geometric product), for testing whether a multivector is a blade or versor, and more such elementary capabilities.
In Chapter 22: Specializing the Structure for Efficiency, we discuss in detail how we used generative programming techniques to construct our own software Gaigen2. It enables using geometric algebra at the high-level for the specification of geometrical operations, and uses its structure in a code generator to produce low-level coordinate operations with an efficiency similar to the best classical solutions. This is demonstrated by some benchmark experiments.
The book contains appendices giving the detailed proofs of some important statements, and a convenient overview of the more useful definitions and formulas. Each Chapter ends with a 'Further Reading' section, relating its contents to the most relevant literature provided in the References. A 14-page index helps you to navigate the book effectively.


